Jawaban Buku Matematika Kelas 8 Ayo Kita Berlatih 1.5 Hal 30 Perhatikan Pola Berikut

Ayo Kita Berlatih 1.5 Semester 1

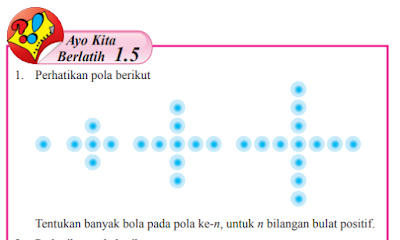
1. Perhatikan Pola Berikut
Tentukan banyak bola pada pola ke-n , untuk n bilangan bulat positif

2. Perhatikan Pola Berikut
Tentukan banyak bola pada pola ke-n , untuk n bilangan bulat positif

3. Perhatikan susunan bilangan berikut. Susunan bilangan berikut dinamakan pola bilangan pascal, karena ditemukan oleh Blaise Pascal. Bilangan di baris ke-2
adalah hasil penjumlahan dari dua bilangan pada baris ke-1. Tentukan jumlah
bilangan pada baris ke-n pada pola bilangan pascal berikut.
1
1 1 Baris ke-1
1 2 1 Baris ke-2
1 3 3 1 Baris ke-3
1 4 6 4 1 Baris ke-4
1 5 10 10 5 1 Baris ke-5

4. perhatikan bilangan bilangan yang dibatasi oleh garis merah berikut. jika pola bilangan tersebut diteruskan hingga n,untuk n bilangan bulat positif,tentukan :
a.jumlah bilangan pada pola ke-n
b.jumlah bilangan hingga pola ke-n

5. perhatikan gambar noktah -noktah berikut.a. Apakah gambar di atas membentuk suatu pola?Jelaskan . b. Tentukan banyak noktah pada 5 urutan berikutnya

6. Tentukan banyak lingkaran pada pola ke 100 pada pola berikut

7. Tentukan banyak lingkaran pada pola ke 10, ke 100, ke n pada pola berikut, untuk sebarang n bilangan bulat positif.Pola 1 = 2
Pola 2 = 6
Pola 3 = 15

8. Tentukan banyak lingkaran pada pola ke-10, 100, n pada pola berikut, untuk sebarang n bilangan bulat positif
2, 8, 12

9. Tentukan banyak lingkaran pada pola ke-10, 100, n pada pola berikut, untuk sebarang n bilangan bulat positif Pola 1= 3 Pola 2=6 Pola 3= 10

10. Perhatikan pola bilangan berikut.1/2 , 1/6 , 1/12
a.nyatakan ilustrasi dari pola tersebut
b.tentukan pola-N untuk sebarang N bilangan bulat positif

11. Dengan memperhatikan bola-bola yang dibatasi garis merah Tentukan:
a.banyak bola pada pola ke-100
b.jumlah bola hingga pola ke-100

12. tiap tiap segitiga berikut terbentuk dari 3 stik. dengan memerhatikan pola berikut tentukan banyak stik pada pola ke 10 ke 100 dan ke n untuk sebarang n bilangan bulat positif

13. Dengan memperhatikan pola berikut, tentukan : 1/2 + 1/6 + 1/12 + ... + (pola ke-n)
a. 3 pola berikutnya
b. pola bilangan ke-n. Untuk sembarang n bilangan bulat positif
c. Jumlah hingga bilangan ke-n. Untuk sembarang n bilangan bulat positif

Kunci Jawaban Ayo Kita Berlatih Halaman 30 Semester 1
1. pola 1 :

U1 = 1

pola 2:

U2 = 5

pola 3:

U3 = 9

pola 4:

U4 = 13

Selisihnya:

U2-U1 = 5-1 = 4

U3-U2 = 9-5 = 4

Jadi barisan tersebut memiliki beda sama yaitu 4

b = 4

Suku ke-n

a = 1

Un = a+(n-1)b

     = 1+(n-1)4

     = 1+4n-4

     = 4n-3

2. 1, 3, 7, 13, 21...

\/  \/  \/  \/

 2  4  6  8 --> b = 2

   \/   \/  \/

   2    2  2 ---> c

Rumus suku ke-n

Un = a + (n - 1) b + ¹/₂ (n - 1)(n - 2) c

Dimana :

Un = suku ke-n

a = suku pertama

b = beda tingkat 1

c = beda tingkat 2

Mari kita terapkan pada soal!

Apabila diurutkan dari yang paling sedikit, bola-bola pada gambar membentuk barisan 1,5,13,25,...

1    5  13   25   ....

 \/   \/    \/

  4   8   12           

    \/    \/

     4     4

a = 1

b = 8 - 4 = 4

c = 4

Un = a + (n - 1 )b + ¹/₂ (n - 1)(n - 2)c

Un = 1 + (n - 1 ) {4)+ ¹/₂ (n - 1)(n - 2)(4)

Un = 1 + 4n - 4 + 2 (n² - 3n + 2)

Un = 1 + 4n - 4 + 2n² - 6n + 4

Un = 2n² + (4n - 6n)  + (1 - 4 + 4) 

Un = 2n² + (-2n) + 1

Un = 2n² - 2n + 1

3. Penjumlahan bilangan-bilangan pada setiap baris dalam segitiga Pascal akan menunjukkan barisan bilangan.
Mari kita lihat penjumlahan pada setiap baris.
                            1                                      → 1 = 2⁰
                       1         1                                 → 1 + 1 = 2 = 2¹
                  1         2          1                          → 1 + 2 + 1 = 4 = 2²
            1          3         3           1                   → 1 + 3 + 3 + 1 = 8 = 2³
     1           4         6          4          1              → 1 + 4 + 6 + 4 + 1 = 16 = 2⁴
1          5         10         10         5            1     → 1 + 5 + 10 + 10 + 5 + 1 = 32 = 2⁵

Berdasarkan jumlah bilangan-bilangan pada setiap baris dari bilangan segitiga Pascal tersebut, dapat dinyatakan sebagai berikut.
Dalam pola bilangan segitiga Pascal, jumlah bilangan pada baris ke-n adalah Sn = 2ⁿ ⁻ ¹.

Contoh :
Berapakah jumlah bilangan pada segitiga Pascal pada baris ke-12?

Jawab :
Jumlah bilangan pada baris ke-12 adalah
S₁₂
= 2¹² ⁻ ¹
= 2¹¹
= 2048.


4.

5. Kita hitung banyak noktak yanga ada pada gambar

Barisan bilangan → 1 , 3 , 5 , 7 , …

Selisih antar bilangan → 3 - 1 = 2, 5 - 3 = 2, 7 - 5 = 2, ...

a. Iya, gambar diatas membentuk suatu pola. Karena mempunyai selisih yang sama tiap bilangan yaitu 2 dan barisan bilangan tersebut merupakan bilangan ganjil.

b. Menentukan banyak noktah 5 urutan berikutnya

1 , 3 , 5 , 7 , ...

Banyak noktah urutan ke-5 = 7 + 2 = 9

Jadi banyak noktah 5 urutan berikutnya adalah 9

6. Pola kesatu = 2

Pola kedua = 4

Pola ketiga = 6

pola keempat = 8

a = 2

b = 4 - 2 = 2

rumus umum Un = a + (n - 1)b

Un = 2 + (n - 1)2

= 2 + 2n - 2

= 2n

Pola ke 100

U₁₀₀ = 2.100

= 200

Jadi suku ke 100 dari pola gambar adalah 200 lingkaran.

7. 2 6 15

4 9

5


2a = 5

a = 5/2


3a + b = 4

3(5/2) + b = 4

15/2 + b = 4

b = 4 - 15/2

= 8/2 - 15/2

= -7/2


a + b + c = 2

5/2 - 7/2 + c = 2

c = 4/2 + 7/2 - 5/2

= 6/2


Un = an² + bn + c

= 5/2 n² - 7/2 n + 6/2

= 1/2 (5n² - 7n + 6)


U₁₀ = 1/2 (5.10² - 7.10 + 6)

= 1/2 (500 - 70 + 6)

= 1/2 (436)

= 218


U₁₀₀ = 1/2 (5.100² - 7.100 + 6)

= 1/2 (50000 - 700 + 6)

= 1/2 (49306)

= 24653

8. Pola pertama = 4 lingkaran

Pola kedua = 8 lingkaran

Pola ketiga = 12 lingkaran

Pola pertama = a

a = 4

Beda = pola kedua - pola pertama atau pola ketiga - pola kedua

         = 8 - 4

         = 4

Rumum umum Un = a + (n - 1)b

Un = 4 + (n - 1)4

     = 4 + 4n - 4

     = 4n

Un = 4n

Pola ke-10 atau U₁₀

U₁₀ = 4.10

     = 40

Pola ke-100 atau U₁₀₀

U₁₀₀ = 4.100

      = 400

9. 3      6    10
     3      4
         1

a = 3
b = 3
c = 1

Un = a + (n-1)b + 1/2(n^2 - 3n + 2)c
U10 = 3 + (10-1)3 + 1/2(10^2 - 3(10) + 2)1
        = 3 + 27 + 1/2(72)1
       = 3 + 27 + 36
       = 66

U100 = 3 + (100-1)3 + 1/2(100^2 - 3(100) + 2)1
           = 3 + 297 + 1/2(10.000 - 300 + 2)
           = 300 + 1/2(9702)
           = 300 + 4851
           = 5151

10.

11. A.
u1= 1
u2= 4+4.1
u3= 4+4.3
maka,
un= 4+4(2n-1)
u100= 4+4 (2*100-1)
u100= 4+4 *199
u100= 4+796
u100= 800
B.
Sn=(2n-1)^2
(199)^2
Sn= 39.601

12. A = 3
b = 2

n=10
Un = a + b(n-1)
     = 3 + 2(9)
     = 3 + 18
     = 21

n=100
Un = a + b(n-1)
     = 3 + 2(99)
     = 201

dan

Un = a + b(n-1)
Un = 3 + 2(n-1)
Un = 3 + 2n - 2
Un = 2n + 1

13. 1/2   1/6    1/12  1/20  1/30  1/42
     +4   +6      +8      +10    +12
penyebutnya di tambah dengan pola bilangan genap

          rumus Un nya  pake yg tingkat 2
rumus umum Un tingkat 2--> Un = an² + bn + c
               x     →   2       6       12      20
                    y    →  +4     +6      +8
                          z  →   +2       +2
mencari c ( 2a = z)
2a = c
2a = 2
 a = 1
menacri nilai b ( 3a + b = y)
3a + b = 4
3(1) + b = 4
3 + b = 4
     b = 1
mencari nilai c ( a + b + c = x)
a + b + c = 2
1 + 1 + c = 2
           c = 0
rumus un untuk bilangan genap Un = an² + bn + c
                                                   Un = n² + n  
maka rumus Un di soal  itu
               1
Un = ---------
         n² + n

Berbagi :